Overview

AES(Advanced Encryption Standard) is a symmetric block cipher. It was accepted by NIST as a standard in 2001. Which means it will be used in most of the security systems. The key length of AES is 128, 192, and 256 bits. The encryption process is the same in all three key lengths. The only difference is the key generation process. When I tried to understand and implement AES 256, I found that there is no clear explanation of the key generation progress. At last, I read the official document of AES and found the answer. In this article, I will introduce the key generation process in AES 256.

Key Schedule Structure

In AES 256, the key length is 256 bits, 32 bytes. But the data block length is still 128 bits, 16 bytes, which means that in the first two rounds, we should use different half of the original key.



We can see that the key schedules in different colors are used in different rounds. There are 14 round encryption processes in AES 256. The first 2 key schedules are given by the user. The other 14 key schedules are generated by the first 2 key schedules.

Key Generation Process

Like the key generation process in AES 128, every word(W[n]) in the key schedule needs to be generated by the previous word(W[n-1]) and the last round of word(W[n-8]).

Besides, the first word of the key schedule, W[4*n] has a different way of generation. The other words are generated by XOR the previous word with the word in the previous key schedule, but for the first word, the previous word need to be transformed before XOR. Like the picture below.



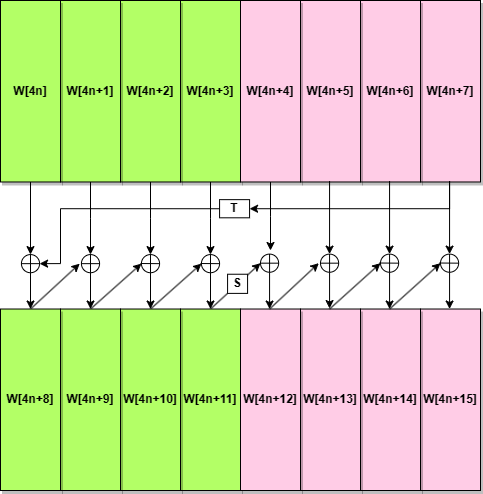
What needs to be aware of is the transform functions for the first word in different colors are different. In other words, the rules for generating W[4*(2n)] and W[4*(2n+1)] are different.

W[4*(2n)]

In the key generation for W[4*(2n)], the T function is the same as the T function in AES 128. It includes 3 steps:

  • RotWord: Rotate the word 1 byte ;
  • SubWord: Substitute each byte of the word with the S-box;
  • Rcon: XOR the first byte of the word with the round constant.

Attention: The round constant isn’t used in the key generation for W[4*(2n+1)], so although AES 256 has more rounds than AES 128, it only needs 7 round constant.

The figure below shows the process of generating W[4*(2n)].



W[4*(2n+1)]

In the key generation for W[4*(2n+1)], the S function just substitutes each byte of the word with the S-box. The figure below shows the process of generating W[4*(2n+1)].



Conclusion

This is all about the key generation process in AES 256. I hope this article can help you understand the key generation process in AES 256. I highly recommend you read the official document’s Appendix A.3. It gives an example of key generation which is very clear and easy to understand. If you have any questions, please leave a comment below. I will reply as soon as possible. Thank you for reading.